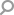El investigador Stan Schein de la Universidad de California parece haber descubierto la existencia de un nuevo tipo de sólido geométrico. Schein se inspiró en el trabajo de Michael Goldberg, quien describió en 1937 un conjunto de cuerpos geométricos que se conocieron como "poliedros de Goldberg", pese a que en realidad no eran poliedros ya que no tenían su caras planas (tenían ángulos internos). Schein encontró estas formas estudiando una proteína llamada Clathrin, esta vez con caras planas. Respetando la labor de Goldberg, decidió llamar a estos nuevos sólidos, "poliedros de Goldberg", los cuales se suman a los sólidos platónicos, los sólidos de Kepler y los sólidos de Arquímides, como las cuatro clases de sólidos geométricos. Tanto Schein como Goldberg pasarán a la historia junto con algunos de los nombres más ilustres de la ciencia y la filosofía.
Este nuevo tipo de poliedros podría tener diversas aplicaciones, desde mejorar la aerodinámica de una pelota de golf hasta el desarrollo de nuevos fármacos —algunos virus, como el de la influenza, tienen una forma similar al poliedro de Goldberg. Mientras tanto disfrutemos contemplar de otra forma matemática, abstracción pura, que aparece consistentemente en la naturaleza.